Lab Links
Projects
Participants
Publications
Collaborators
Alumni
Links
Lead Investigators
Paul Dawson
prd5@cornell.edu
Matt Miller
mpm4@cornell.edu
Contact Us:
web
administrator
Quick Links to Projects
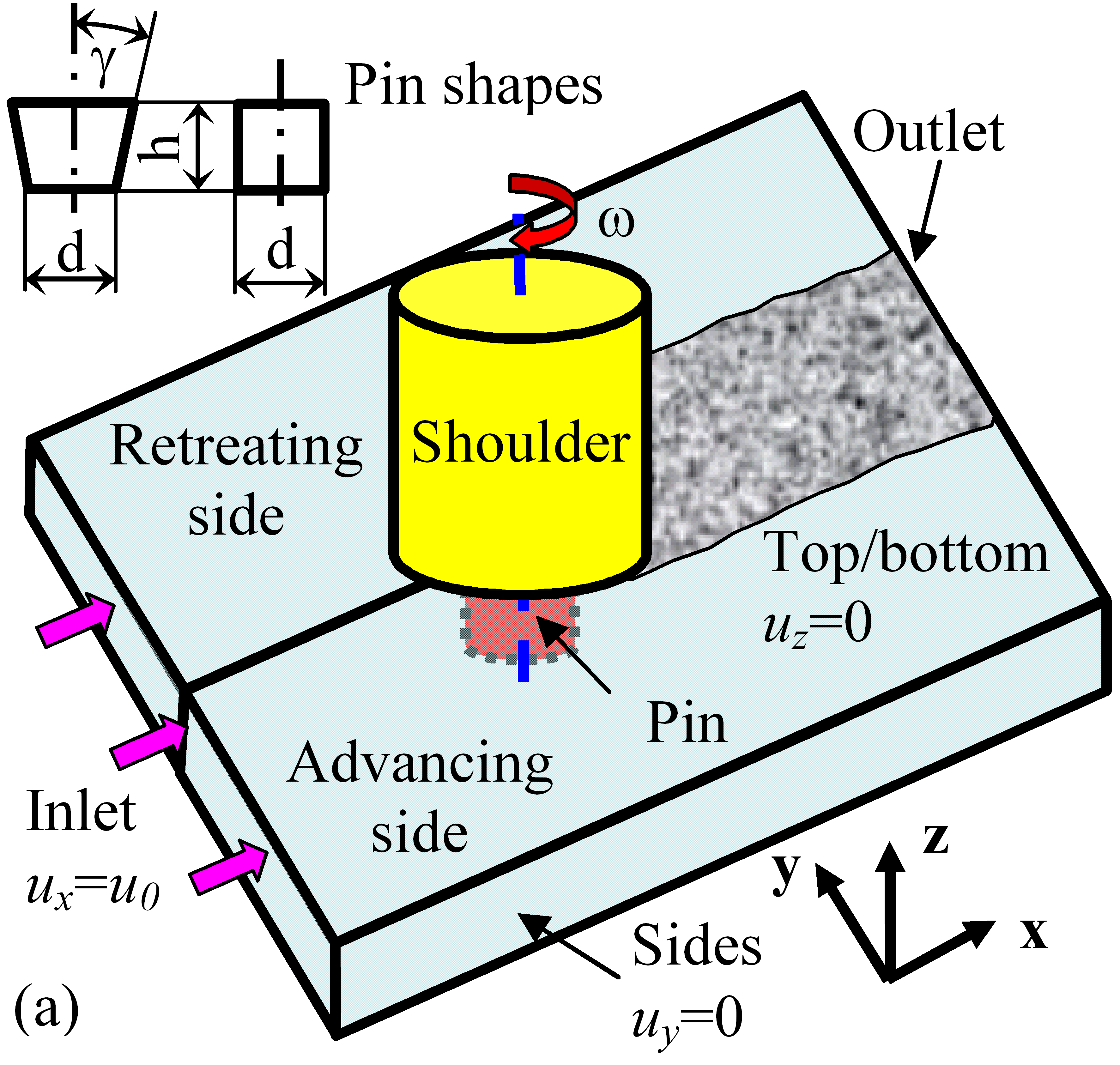
Finite Element Modeling of Friction Stir Welding
(Sponsor: ONR Structural Materials Program)Donald Boyce and Paul Dawson
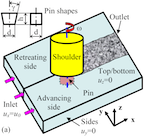
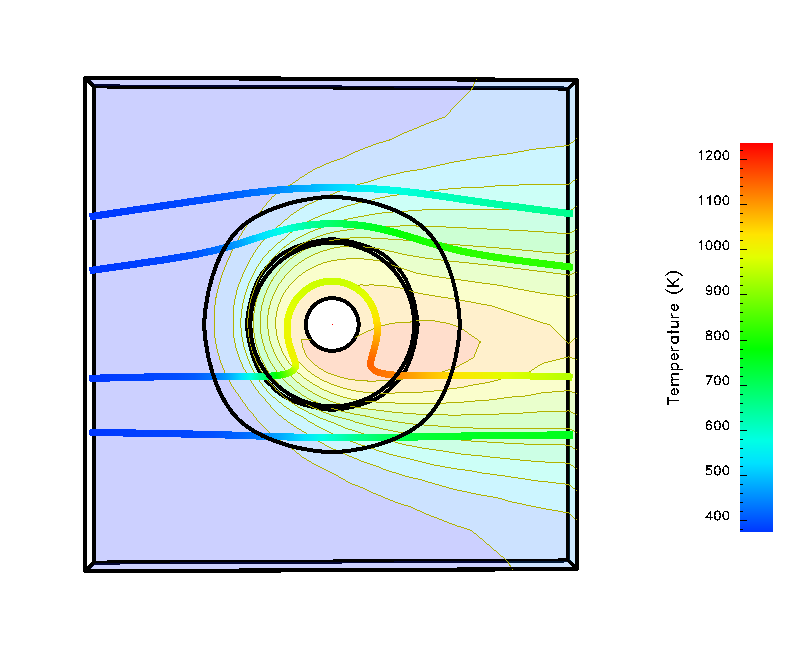
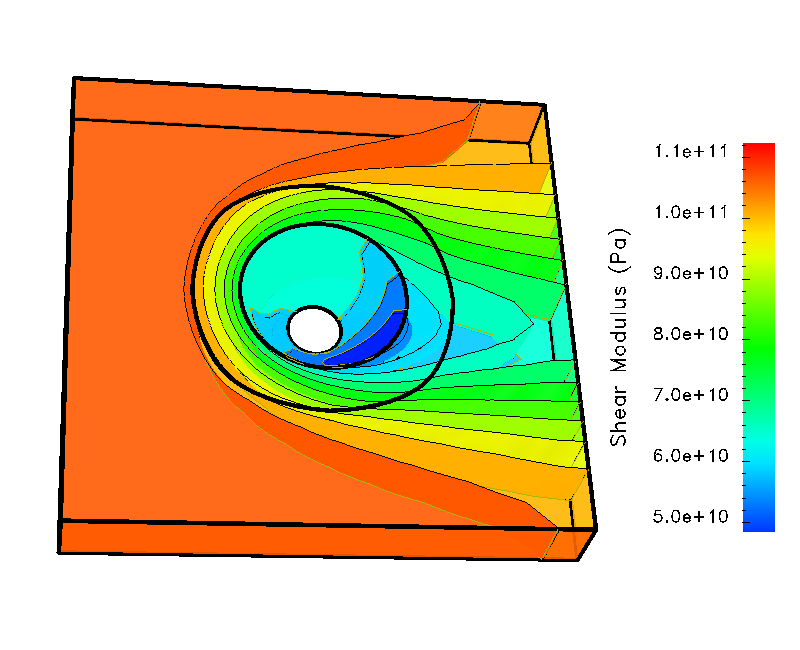
Friction stir welding is a relatively new type of welding process. For aluminum alloys it is already in commercial practice and is proving to be quite effective. For high strength alloys, such as stainless steel and titanium alloys, the process is still under development, but showing considerable promise to deliver superior properties often achieved with solid-state welding. We are actively working on techniques for simulating the process for these classes of materials, particularly the evolution of microstructural variables such as the crystallographic texture. We are using a three-dimensional, thermomechanically-coupled, finite element formulation in which the plastic flow is treated with a state-variable constitutive model. Using streamline integration methods, we track the evolution of the strength, the texture, and the growth of voids. The formation of defects such as internal voids are a serious concern for the integrity of a weld, and our focus in simulating the process is to help identify which welding conditions are the best for avoiding void growth. Shown are typical temperature and strength distributions around the rotating pin used in FSW processes to stir the material as it passes by the pin. Currently we are developing a version of our FSW code for public release. If you are interested in obtaining this code, please contact Donald Boyce (email address available under Participants).
Articles published by our group on this subject include:
- J.-H. Cho, D. E. Boyce, and P. R. Dawson.
Modeling strain hardening and texture evolution in friction stir welding of stainless steel. Materials Science and Engineering A, 398:146-163, 2005. - D. E. Boyce, P. R. Dawson, B. Sidle, and T. Gnaupel-Herold.
A multiscale methodology for deformation modeling applied to friction stir welded steel. Computational Materials Science, 38:158-175, 2006. - J.-H. Cho and P. R. Dawson.
Investigation of texture evolution during friction stir welding of stainless steel. Metallurgical and Materials Transactions, 37A:1147 -1164, 2006. - J.-H. Cho, D. E. Boyce, and P. R. Dawson.
Modeling strain hardening during friction stir welding of stainless steel. Modeling and Simulation in Materials Science and Engineering, 15:486-489, 2007. - Y. He, P. R. Dawson, and D. E. Boyce.
Modeling damage evolution during friction stir welding of stainless steel. Journal of Engineering Materials and Technology, 130:021006-1-021006-10, 2008. - J.-H. Cho, D. E. Boyce, and P. R. Dawson.
Modeling texture evolution during friction stir welding of stainless steel with comparison to experiments. Journal of Engineering Materials and Technology, 130:01007-1-011007-12, 2008.
Coordinated Neutron Diffraction Experiments and Finite Element Simulations to Investigate The Elastic-Plastic Transition Under Multiaxial States of Stress
(Sponsor: ONR Structural Materials Program)Paul Dawson (Cornell), Tito Marin (University of Parma) and Michael Gharghouri (NRC Canada)
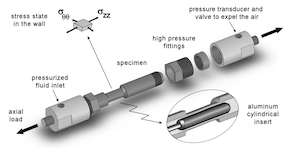
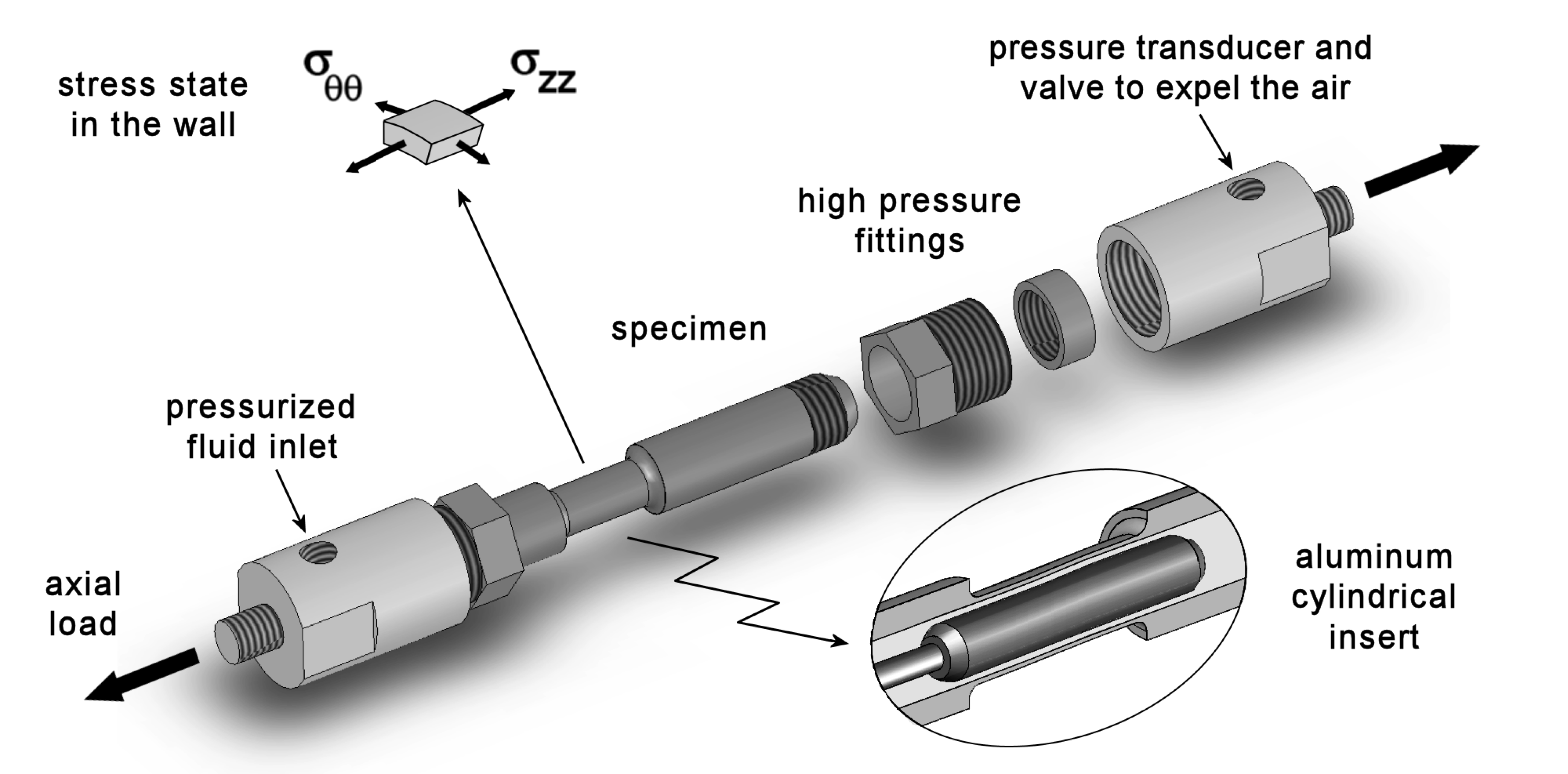
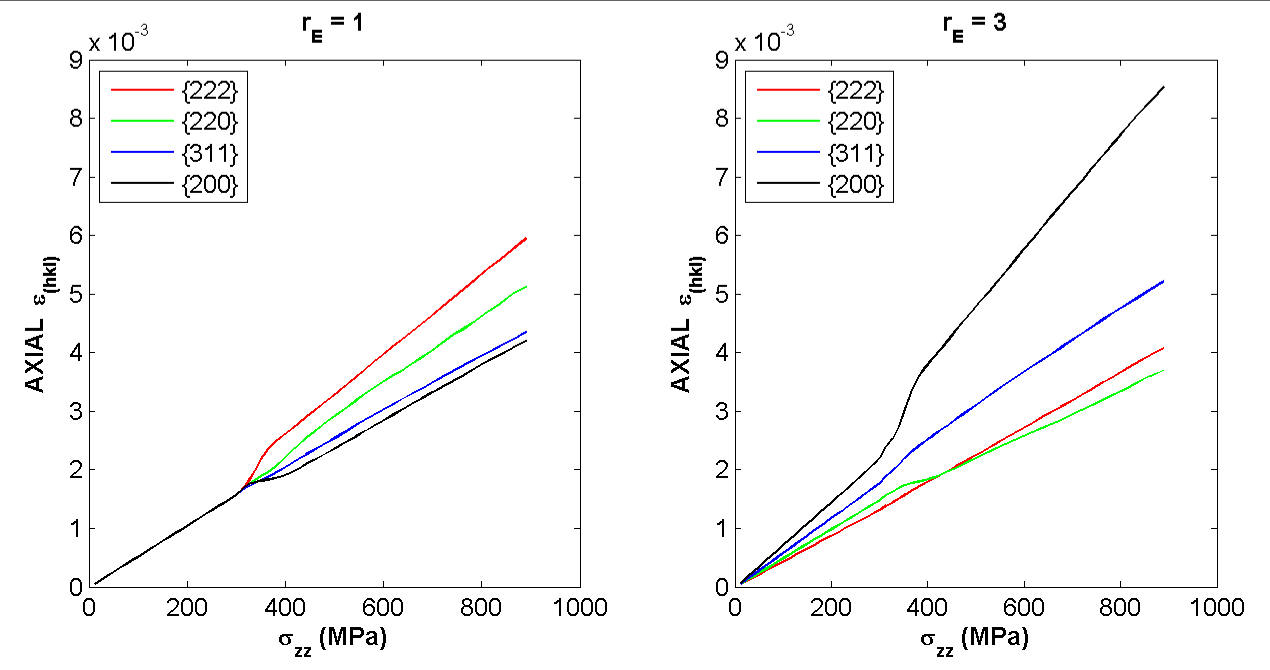
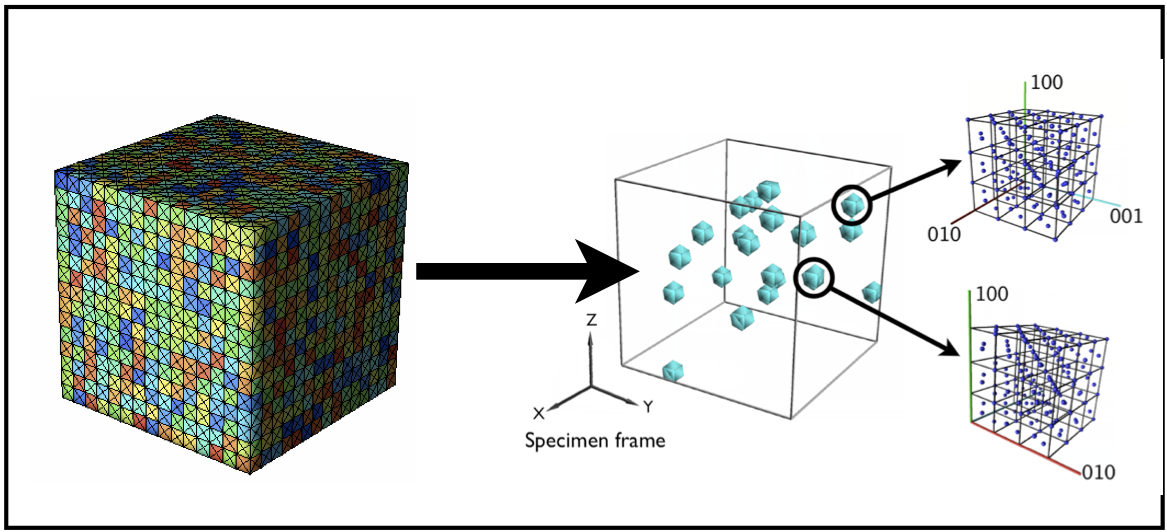
In this project we are investigating the manner in which yielding progresses through a polycrystalline material as it progresses from the elastic regime through the elastic-plastic transition and into fully-developed plastic flow. We are examining how the level of biaxiality of the stress macroscopically influences the transition at the crystal scale. Namely, how the set of yielding depends on crystallographic orientation, beginning with those crystals with the most favorable orientations and terminating when plastic flow extends throughout the material. The important parameter for determining which crystals are more favorably orientated is the crystallographic strength-to-stiffness ratio, which depends not only not crystal class (cubic versus hexagonal, for example), but also on the strength of the anisotropy exhibited by a particular material (elastic anisotropy of aluminum versus copper, for example). The investigation uses coordinated finite element simulations of polycrystals and neutron diffraction experiments with in situ mechanical loading to generate and interpret a picture of the evolving stress state under various degrees of stress biaxiality. A schematic of the sample employed is shown to indicate how the stress biaxialty can be imposed by controlling the internal pressure and axial load on a thin-walled cylindrical sample. Custom fixtures and loading capabilities were developed especially for these experiments to facilitate pressurizing the sample concurrently with applying axial load in a tension-compression load frame. The design enabled us to probe the wall of the sample with a monochromatic neutron beam and collect diffraction data for a number of combinations of scattering vector and crystallographic reflection. The finite element mesh shows a representation of a portion of the gage section with individual dodecahedral grains discretized with higher-order tetrahedral elements. To relate the results of the simulation with the experimental data, we compare computed and measured lattice strains for crystals lying along the same crystallographic fibers as the experiment progresses The stress biaxiality alters the relative values of the principal components of the stress and consequently changes the active vertices of the single crystal yield surface. By carefully comparing and contrasting the evolution of the lattice strains as we change the overall level of biaxiality, we learn more about why the stress biaxialty alters the distribution of crystal stresses over the volume of the polycrystal, changing the apparent strength-to-stiffness ratio, and modifying the progression of plastic from through a polycrystal. The issues examined in this investigation are central to a more fundamental understanding of the inelastic properties of engineering alloys that is necessary to improve their mechanical properties.


Several articles are available on the this and related projects, including:
- P. Dawson, D. Boyce, S. MacEwen, and R. Rogge.
Residual strains in HY100 polycrystals: Comparisons of experiment and simulations. Metallurgical and Materials Transactions A, 31:1543 - 1555, 2000. - P. Dawson, D. Boyce, S. MacEwen, and R. Rogge.
On the influence of crystal elastic moduli on computed lattice strains in AA5182 following plastic straining. Materials Science and Engineering A, 313(1-2):123 - 144, 2001. - P. R. Dawson, D. E. Boyce, and R. Rogge.
Correlation of diffraction peak broadening and crystal strengthening in finite element simulations. Materials Science and Engineering A, 399(1-2):13-25, 2005. - P. R. Dawson, D. E. Boyce, and R. Rogge.
Issues in modeling heterogeneous deformations in polycrystalline metals using multiscale approaches. Computer Modeling in Engineering and Sciences, 10(2):123- 141, 2005. - T. Marin, P. R. Dawson, M. A. Gharghouri, and R. B. Rogge.
Diffraction measurements of elastic strains in stainless steel subjected to in situ biaxial loading. Acta Materialia, 56:4183-4199, 2008.
Developing a Robust and General System for Organizing and Archiving Materials Data
(Sponsor: ONR and DARPA)Donald Boyce, Paul Dawson and Matt Miller
In this project, we are working to design and implement a software system for organizing, archiving, and sharing large, diverse materials data sets. To meet expectations, the system should be capable of the following: (1) disseminating data in their completeness beyond what is possible by the publication of images,plots, or discussions found in archival journal publications; (2) enabling activities, such as modeling, that integrate complementary but distinct data sets; (3) facilitating technical interactions among researchers who bring a wide array of resources to bear on a common topic; and (4) archiving data so that they may be reliably accessed by any researcher, whether that person is the data contributor or someone else who is work- ing in a laboratory or on a project unrelated to that of the contributor.
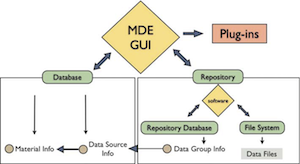
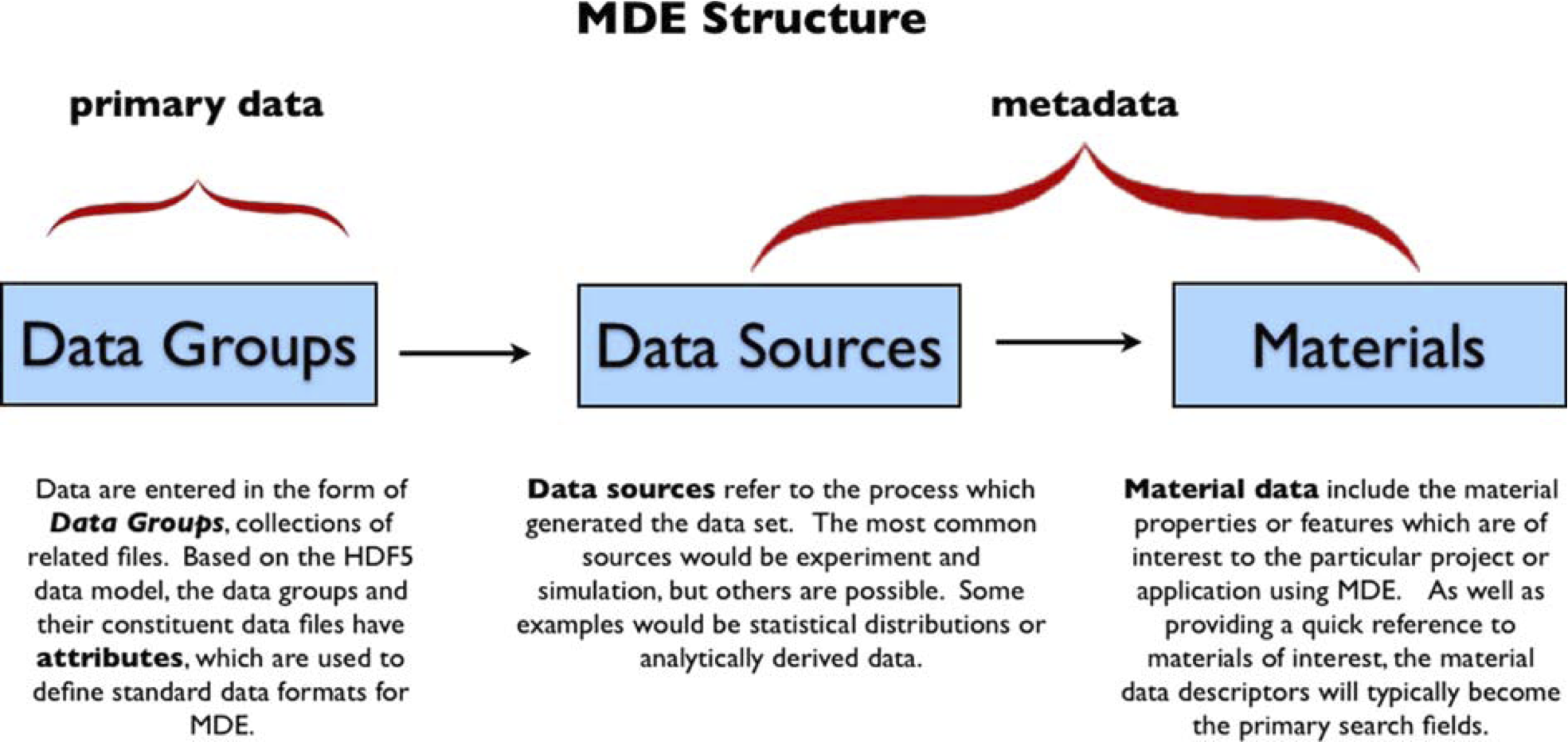
Our system for managing materials data is called the material data environment (MDE). Its basic structure makes it highly configurable to a specific project. Information retained in the MDE is separated into two categories: the primary data and the metadata, as illustrated in the first figure below. The primary data are actual material data sets resulting from experiments, simulations, or other processes. The metadata are information about the primary data, including their origin and descriptions of associated materials. The metadata are stored on a host computer in a relational database, which will be referred to as the metadata database and is accessible remotely to the users. The metadata are further separated into two parts: the material metadata, which hold information regarding the identification and description of materials represented in the MDE, and the data source metadata, which hold similar information associated with the data sources. In contrast, the primary data are saved in the data repository, which uses both a file system to store raw data sets and a relational database (the repository database) to mark those data sets with attributes describing their structure and contents. The repository database and the metadata database are only connected through data source references in the repository database. The focus of the MDE is the archiving and sharing of the primary data; the organization is provided by the metadata, which allow data to be searched by material and data origin.
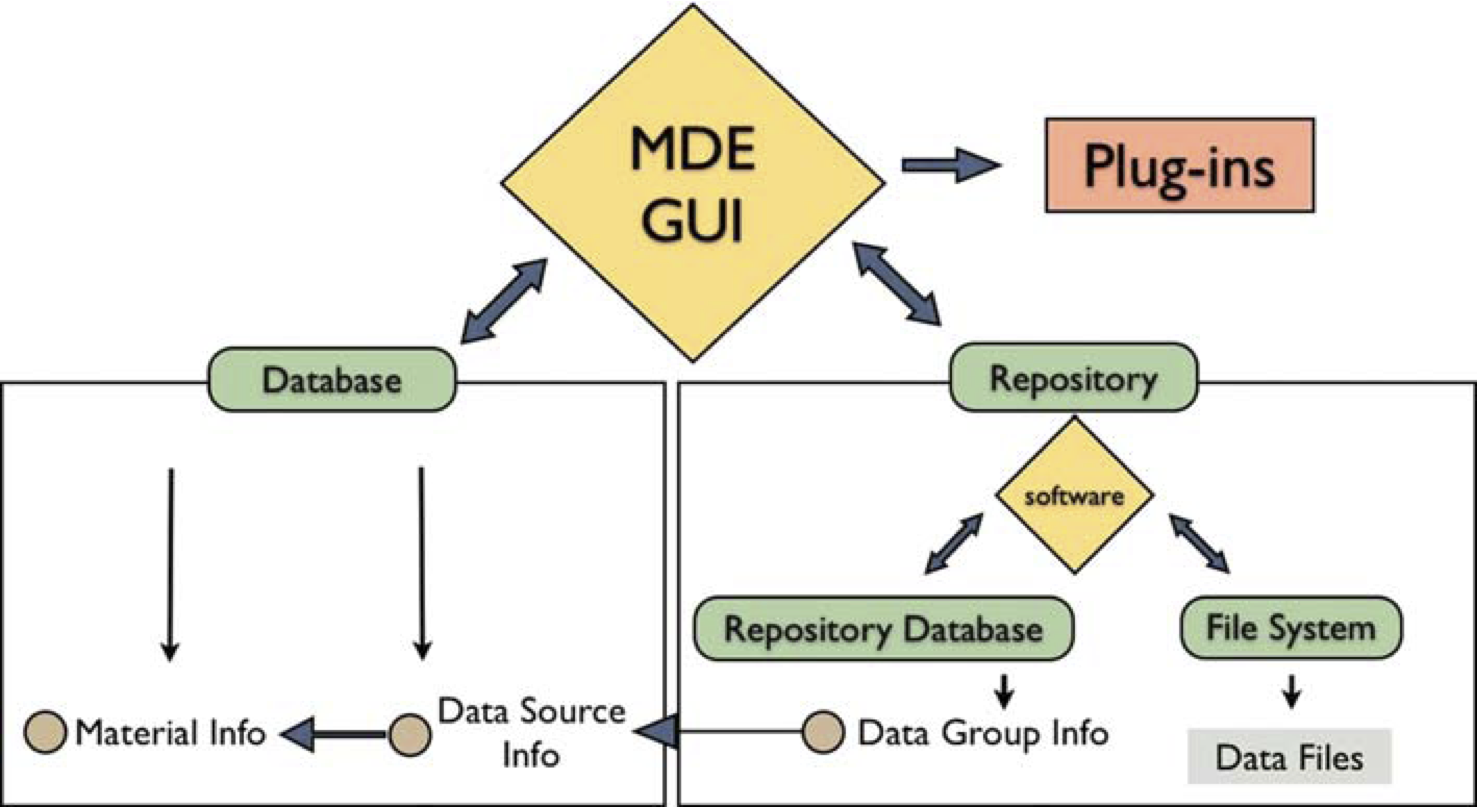
Just as the MDE structure logically has two parts, the software implementation also has two components: the MDE GUI, a graphical application for user interaction with the MDE; and the repository server, a program that manages the data repository. The components and their roles are shown in second figure below. The MDE GUI automatically generates and presents forms to the user for entering metadata. For entering primary data, special data entry forms are developed for each data format. On any actual transfer of data files, the repository server, which coordinates the repository database and the file system, is invoked by the MDE GUI. Additionally, the MDE GUI has a programming interface to allow plug-ins, external modules, or pro- grams that enhance the data processing capability.
A full description of a prototype system is provided in:
- D. E. Boyce, P. R. Dawson, and M. P. Miller.
The design of a software environment for organizing, sharing and archiving materials data. Materials Science and Engineering A, 40:2301-2318, 2009.
A related development that formed part of the basis for the organization of this archiving system is reported in:
-
P. R. Dawson, M. P. Miller, T.-S. Han, and J. Bernier.
An accelerated methodology for the evaluation of critical properties in polyphase alloys. Metallurgical and Materials Transactions, 36A:1627-1641, 2005.
Currently we are working with others on implementations to support specific projects and laboratories.
Modeling Texture Evolution in Polycrystals Using Finite Element Formulations
(Sponsor: ONR)Paul Dawson, Tito Marin, Romain Quey and Donald Boyce
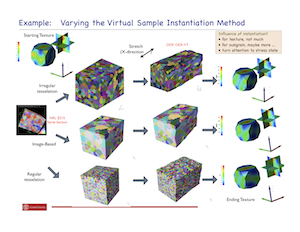
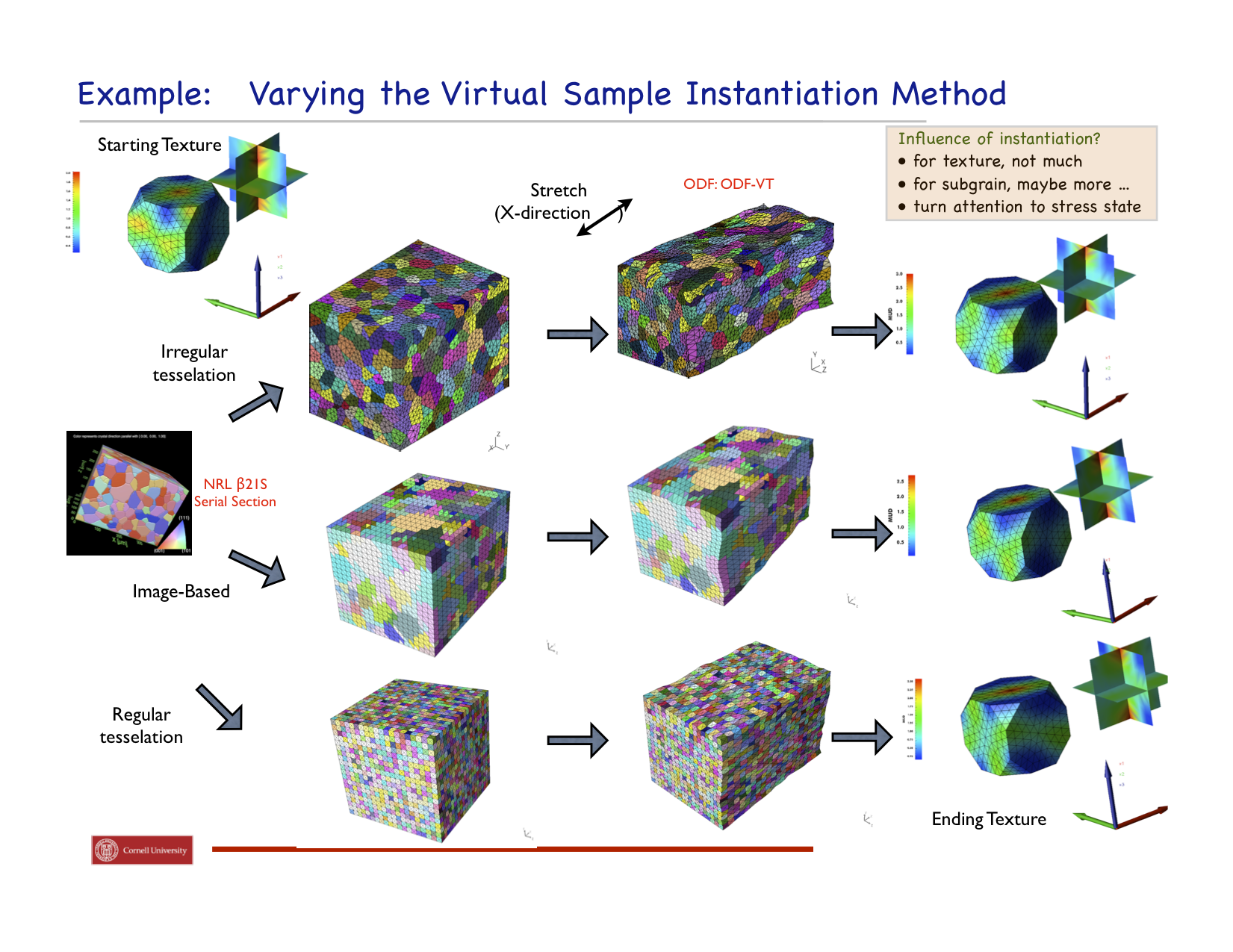
We have had a continuing effort to better understand the evolution of texture in polycrystalline materials using finite element formulations based on crystal plasticity to compute lattice reorientations under large strain deformations. As part of the larger effort, we have looked at issues associated with the assumptions regarding strain hardening as well as issues related to the methods of instantiation of virtual polycrystals used to represent polycrystalline aggregates. For example, the figure below shows three virtual polycrystals that were instantiated by distinct methods. The first is a regular tessellation, second an irregular tessellation, and the third an image-based reconstruction. All represent the real material with statistically-equivalent crystallographic textures. However, the grain shapes are quite different, and as a consequence, the statistics relative to average numbers of neighbors differ between the three samples. The evolved texture is shown as well for each case following an equal amount of deformation in extensional. While the major texture components remain the same (owing to the location of equilibria), subtle difference arise from the differences in morphology and/or initialization. We are also examining the attributes of the intragrain lattice misorientations. The grain interactions are sources of heterogeneity of the stress distribution. Spatial variations in the stress give rise to activation of different combinations of slip systems, which in turn, causes differences in lattice re-orientation. We are using a correlation tensor developed by Barton as part of his dissertation to study the orientational dependence of the misorientations. Usually there is one direction within a crystal in which there is a systematic twist to the lattice, but this direction only correlates to the loading direction for certain crystal types. Also shown below is a depiction of components of the correlation tensor. For more details see the cited articles.
Articles that have been published by members of our group on this subject include:
- A. J. Beaudoin, P. R. Dawson, K. K. Mathur, and U. F. Kocks.
A hybrid finite element formulation for polycrystal plasticity with consideration of macrostructural and microstructural linking. International Journal of Plasticity, 11:501 - 521, 1995. - G. B. Sarma and P. R. Dawson.
Effects of interactions among crystals on the inhomogeneous deformations of polycrystals. Acta Metallurgica et Materialia, 44:1937 - 1953, 1996. - D. P. Mika and P. R. Dawson.
Polycrystal plasticity modeling of intracrystalline boundary textures. Acta Materialia, 47(4):1355 - 1369, 1999. - N. R. Barton and P. R. Dawson.
On the spatial arrangement of lattice orientations in hot rolled multiphase titanium. Modeling and Simulation in Materials Science and Engineering, 9:433-463, 2001. - M. Miraglia, P. Dawson, and T. Leffers.
On the influence of mechanical environment on the emergence of brass textures in fcc metals. Acta Materialia, 55:799-812, 2007. - A. Kumar and P. R. Dawson.
Dynamics of texture evolution in face-centered cubic polycrystals. Journal of the Mechanics and Physics of Solids, 57:422-445, 2009. - P. Dawson, J. Gerken, and T. Marin.
Modeling heterogeneous intra-grain deformations using finite element formulations. In S. Ghosh and D. Dimiduk, editors, Computational Methods for Microstructure-Property Relationships. Springer, in press.
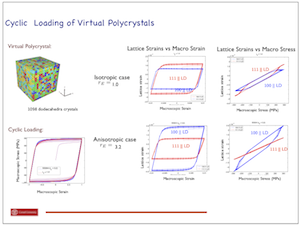
Determining the Evolution of Crystal-Scale Stress Distributions During Cyclic Loading
(Sponsor: AFOSR)Jay Schuren, Su-Leen Wong, Matt Miller and Paul Dawson
Fatigue damage is one of the principal reasons for retiring a component. In spite of considerable research devoted to fatigue, many of the processes by which fatigue damage initiates are inadequately understood. The main reason for this situation has been an inability to either measure or compute stress at the scale where the damage initiates -- within crystals. Recent advances in computation and instrumentation have provided the means to address the issue of crystal-scale stress distributions in polycrystalline alloys. This project involves a highly coordinated program of complementary simulations and experiments that exploit these advances. Using synchrotron X-ray diffraction, we are measuring lattice strains under dynamic loading conditions. A schematic figure of the measurement technique is shown below for collecting data associated with a particular set of scattering vectors. Over the course of a cyclic loading history the lattice strains evolve, giving us direct observations of how stress is changing within particular sets of crystals, as shown in the second figure. Using finite element simulations of polycrystals we are modeling the material under the same dynamic loading conditions and then extract lattice strains from crystals that satisfy the diffraction conditions observed in experiment, as shown schematically below. In the final figure, one sees that the simulations show a dramatic influence of elastic anisotropy on the lattice strain hysteresis loops. The simulations and experiments are being closely coordinated to support each other in developing a fundamental understanding of how stresses evolve during cyclic loading. Through this research, we shall seek to learn why defects are prone to advance toward microcracks in some regions of the microstructure and how the multiaxial stress state at the crystal scale influences that process. This knowledge is critical to attaining a more fundamental understanding of fatigue that will enable us to reduce conservatism in design and to increase reliability in operation of load-bearing components.
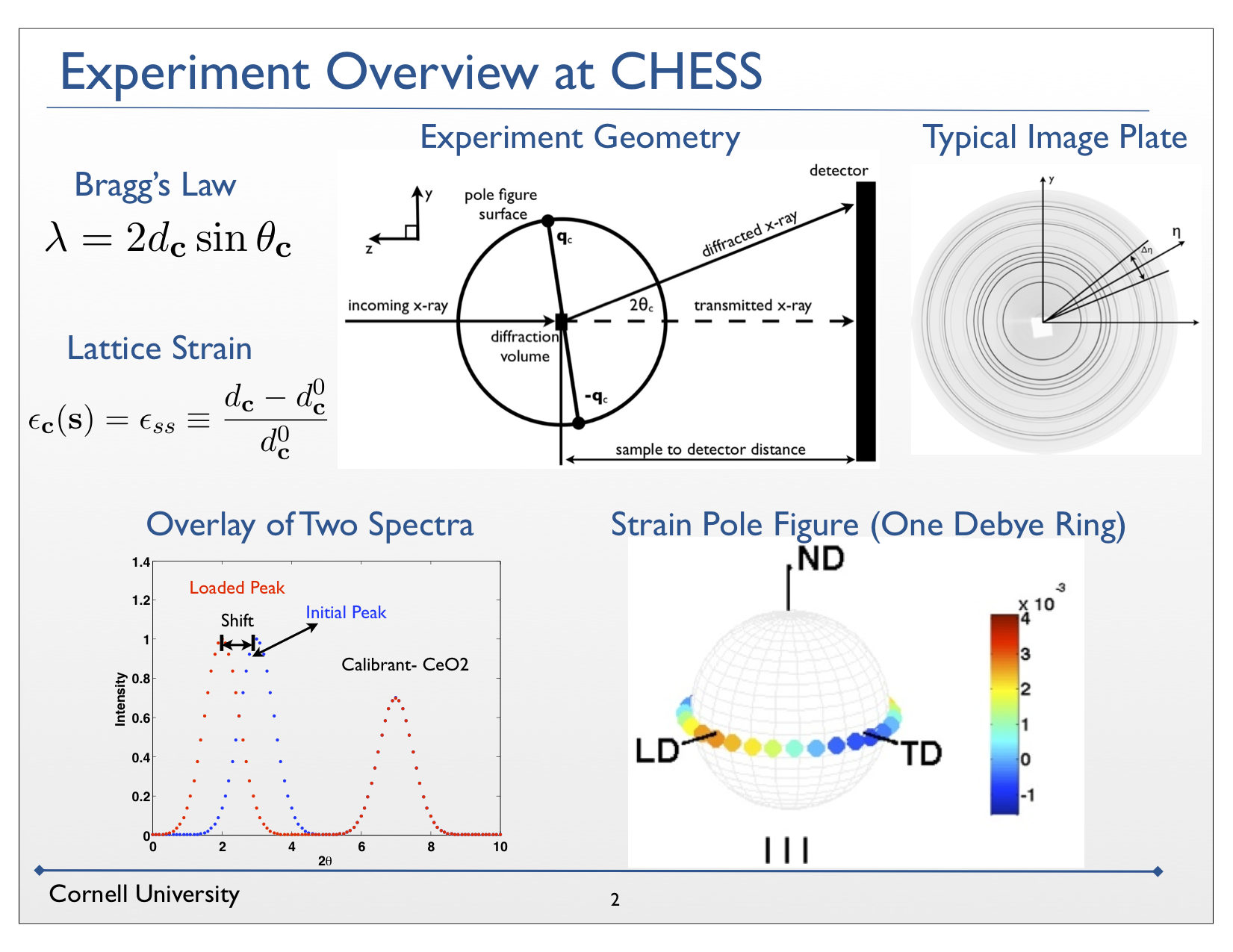
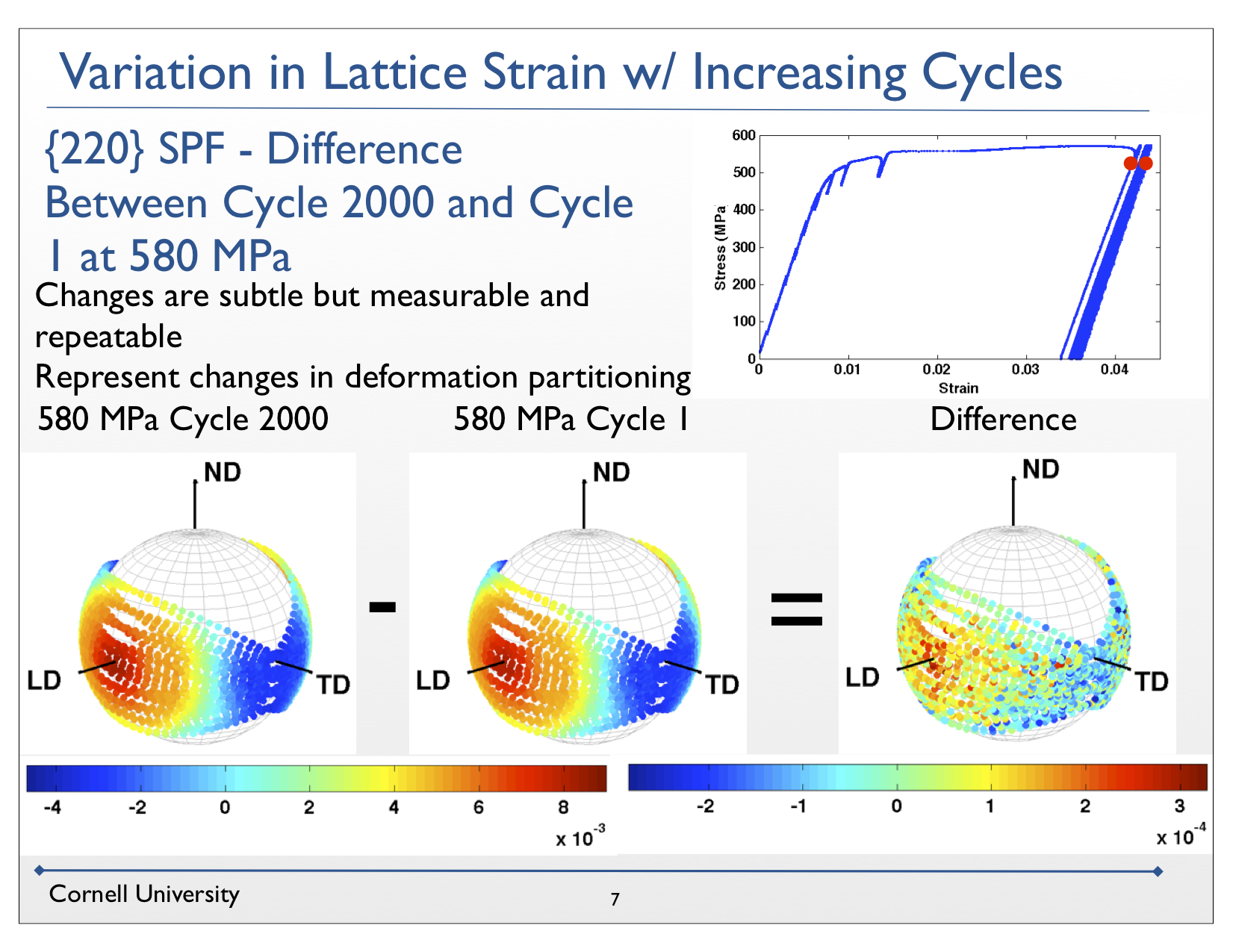
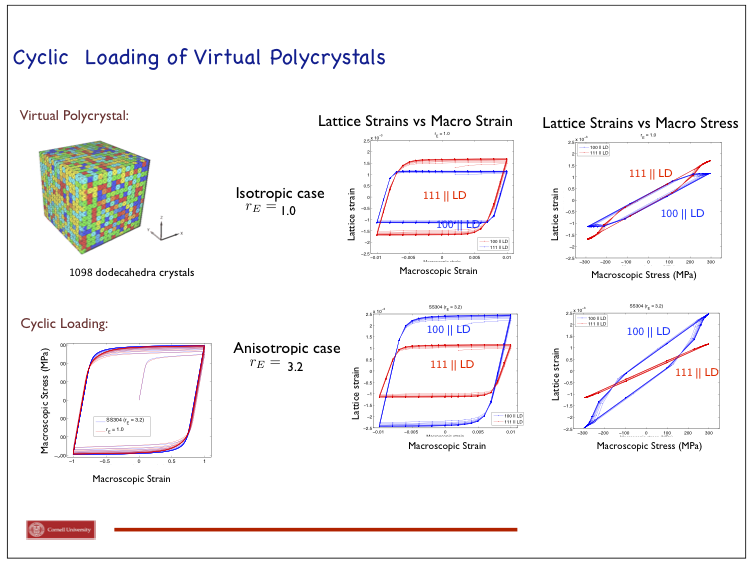
Papers related to our research on fatigue, from this project and earlier ones, include:
- H. Turkmen, P. R. Dawson, and M. P. Miller.
The evolution of crystalline stresses of a polycrystalline metal during cyclic loading. International Journal of Plasticity, 18:941-969, 2002. - H. Turkmen, R. Loge, P. R. Dawson, and M. P. Miller.
On the mechanical behavior of AA7075-T6 during cyclic loading. International Journal of Fatigue, 25:267-281, 2003. - S. L. Wong and P. R. Dawson.
Infuence of directional strength-to-stiffness on the elastic-plastic transition of FCC polycrystals under uniaxial loading. Acta Materialia, 58:1658-1678, 2010.
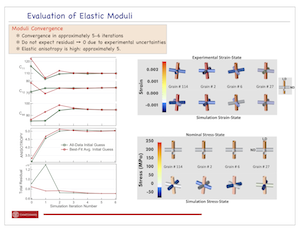
Probing the Behavior and Properties of Polycrystalline Materials Grain-by-Grain
(Sponsor: ONR and DARPA)Matt Miller, Paul Dawson, Donald Boyce and Christos Efstathiou
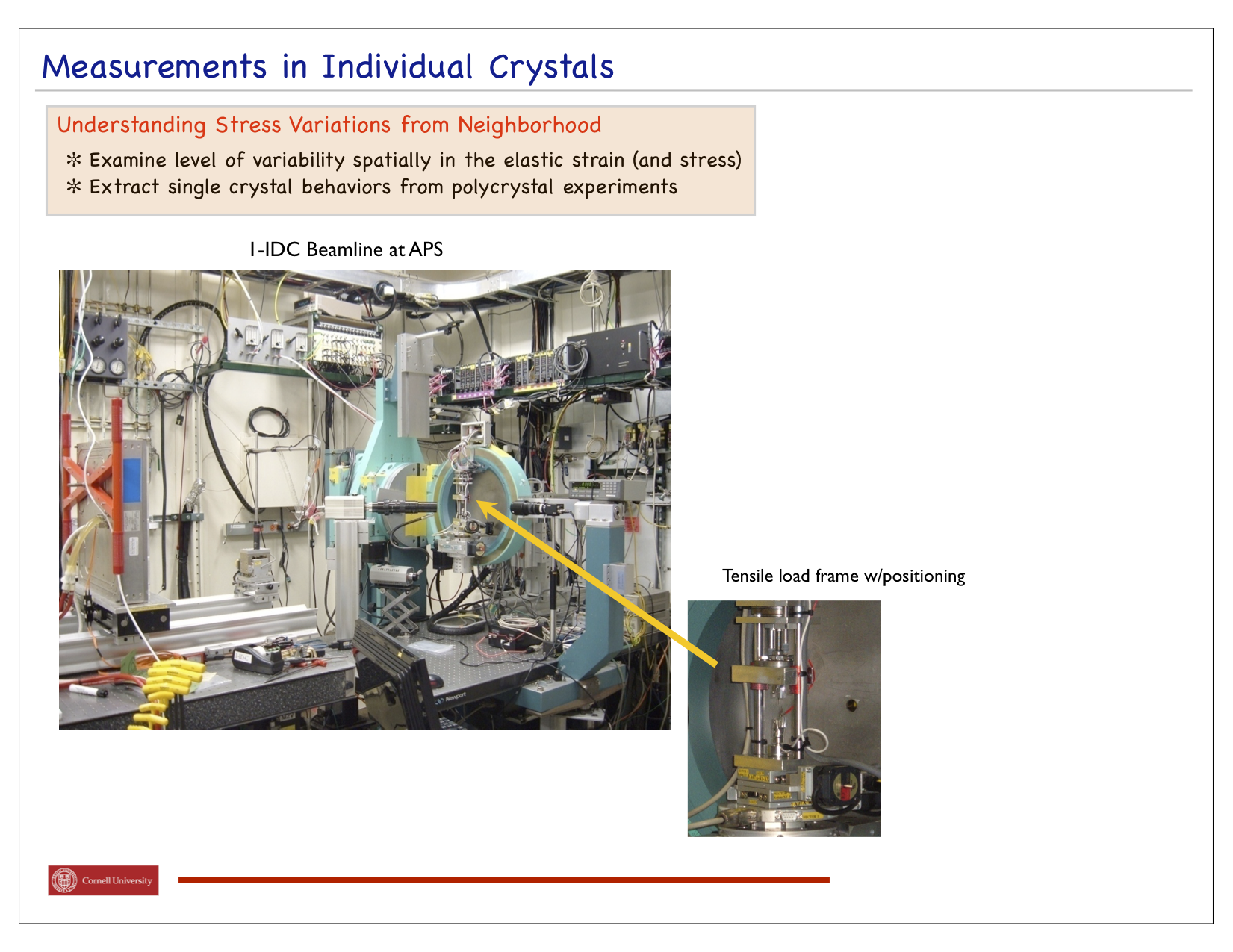
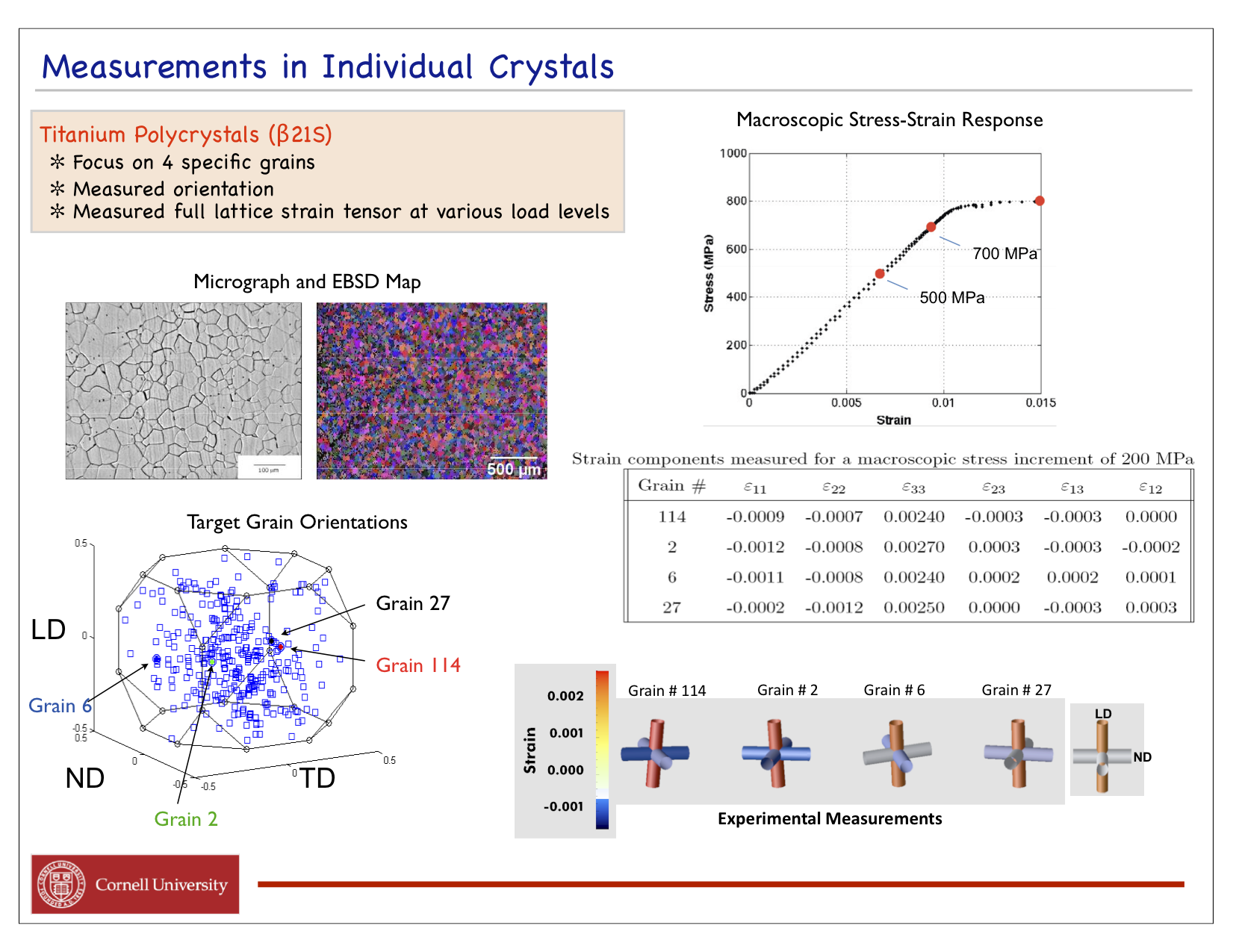
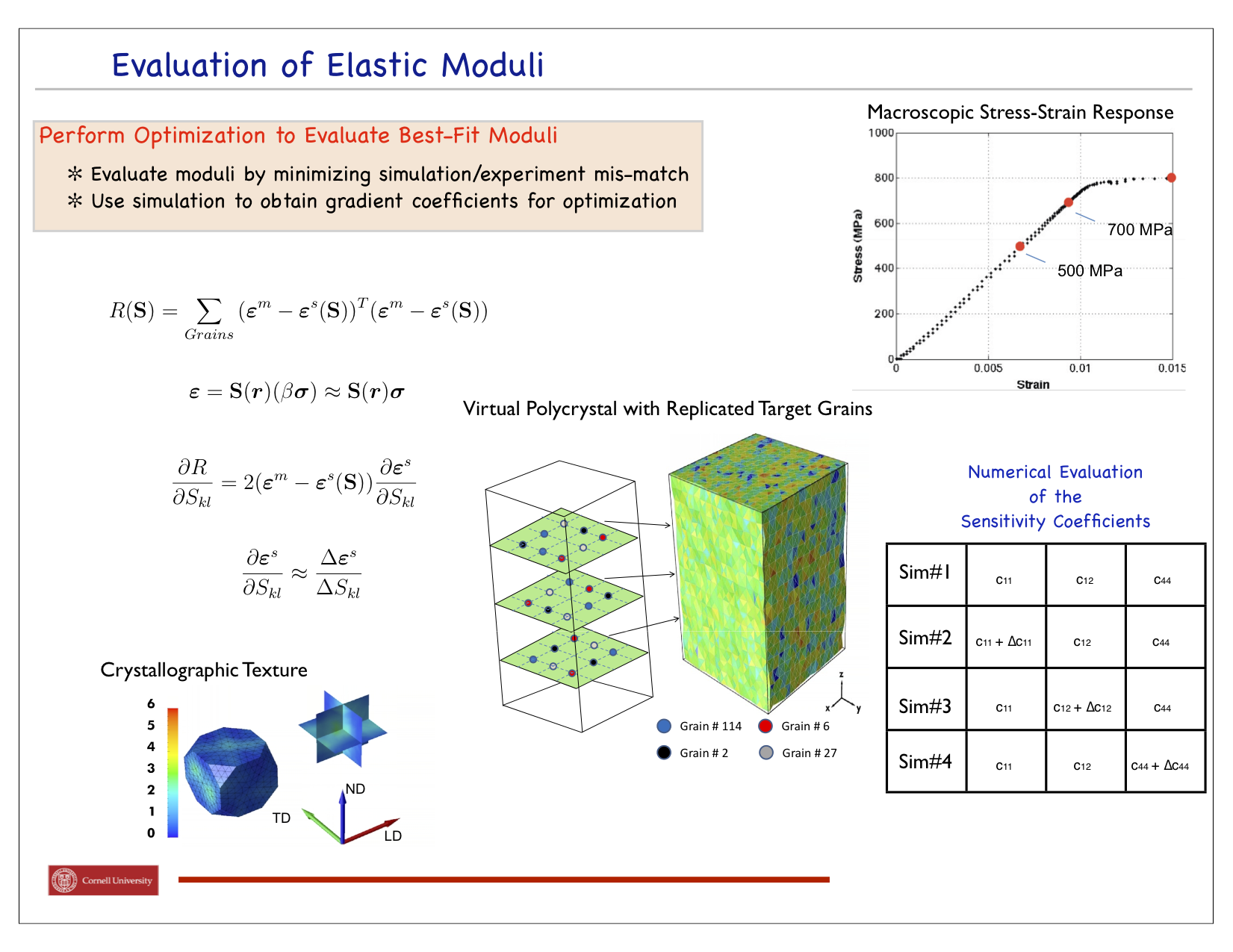
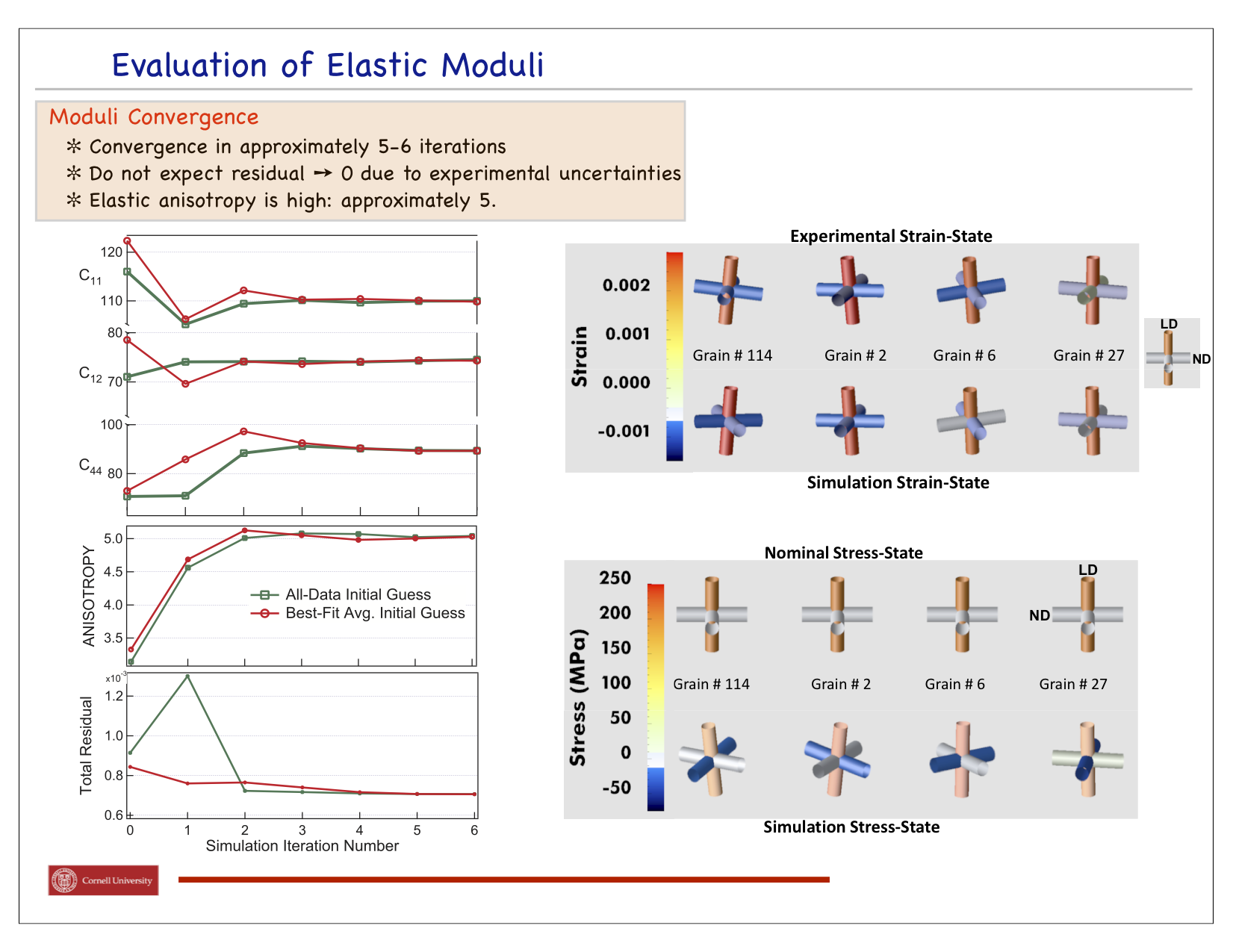
The end goal of this project is to both measure and compute the elastic strain tensor in every grain of a deforming sample comprised of thousands of crystals. With such comprehensive knowledge of the mechanical response of an engineering alloy we will have the capability to identify when and how a material distributes stress when loaded. Further, we'll be able to better understand where life-ending defects originate and what the stress was when the failure began. Progress to date has been to measure lattice strain tensors for a select number of crystals distributed over the sample's volume. We have used this data in conjunction with crystal-by-crystal finite element simulations to determine the optimal choice of elastic moduli for the materials, in this case a titanium alloy. Shown in the first figure is the experimental apparatus developed for use at the Advanced Photon Source. It consists of a small load frame that is attached to a positioning ring so that the loaded sample can be illuminated by the x-ray in many orientations. The second figure identifies the orientations of grains within the sample and lists the lattice strain tensors in four grains at several load levels. The optimization procedure developed for extracting the moduli is outlined in the following figure, depicting how the finite element simulations are used to compute sensitivity coefficients for the optimization procedure. The final figure indicates the improving estimates of the moduli as the optimization procedure converged on a final estimate.
Using Synchrotron X-rays and a Biscale Material Representation to Evaluate Processing-Induced Stress States in Aircraft Engine Alloys
(Sponsor: DARPA)Matt Miller, Paul Dawson, Cornell; Jim Williams, The Ohio State University
The heterogeneous thermal and mechanical loading conditions experienced by titanium engine components during processing induce non-uniform stress fields. Unaccounted for, these residual stresses make life prediction under fatigue conditions practically impossible. Enormous factors of safety are employed, which results in gross inefficiencies. Methods for measuring residual stresses have been around for many decades. Diffraction methods have emerged as a very promising method for interrogating internal stresses by quantifying shifts in diffraction peaks produced by straining of the crystal lattice. The problem with x-rays produced by conventional sources such as rotating anodes is the lack of penetration power. The immense promise offered by high energy synchrotron x-rays and area detectors is penetration power and short collection times. We now have the ability to measure lattice strains in many directions using a variety of crystal planes at a material point. Quantification of the three-dimensional lattice strain tensor is now possible. Dealing with the enormous amounts of data produced during a lattice strain experiment is one of the profound challenges for using synchrotron x-ray data to determine residual stress. Using our backgrounds in titanium metallurgy and the use of titanium in aircraft engines, in the development of synchrotron x-ray diffraction mechanical deformation experiments and in the derivation of orientation-based domain representations for elastic-plastic behaviors we will develop a methodology for quantifying the residual stress distribution over a titanium component at the macroscopic (continuum) scale from microscopic (crystal) scale diffraction data gathered at chosen locations. We will employ our techniques for measuring lattice strain distributions in aggregates of loaded polycrystals using high energy synchrotron X-rays; for representing orientation-dependent quantities; and for performing various averaging and projection operations. Using these techniques, we will link the continuum and crystal scale quantities in mathematically rigorous terms. We will carefully control the degrees of freedom in the continuum and crystal scale stress distributions through the manner in which we represent those functions. This project will significantly leverage our AFOSR residual stress project by connecting the synchrotron measurements to more conventional x-ray diffraction tests. In the figure the high profile hybrid disk project is outlined. The techniques we develop here should enable field measurements within components such as the hybrid microstructure. We are currently conducting baseline diffracti4n tests on the Nickel-base alloy LSHR. The challenge of these tests will be the large grain size in the 1170 heat treated material. We have had to employ new data acquisition methods in order to interrogate an acceptable number of crystals.
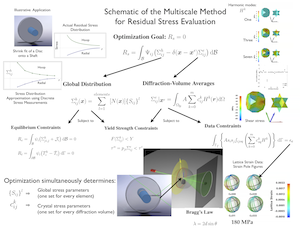
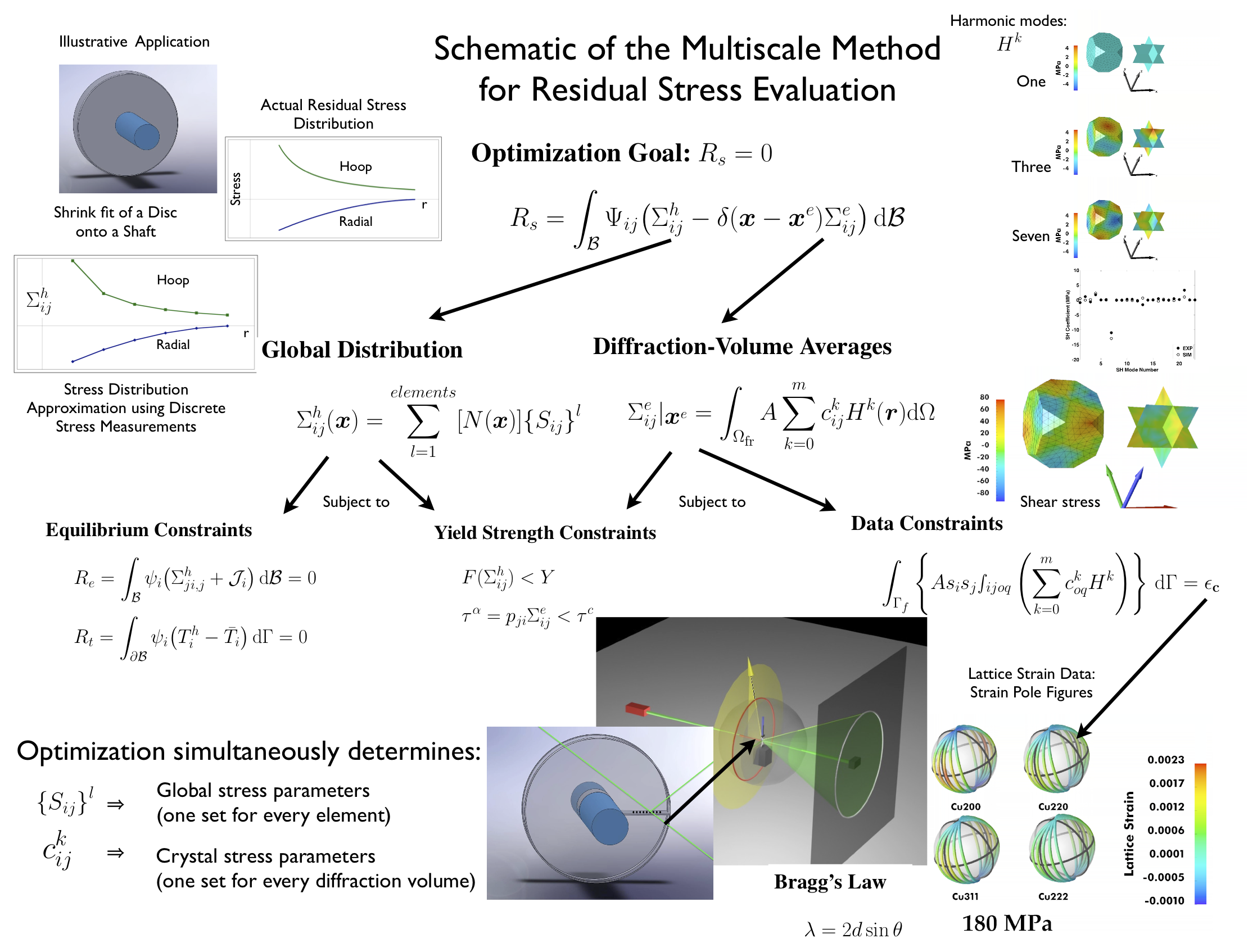
A New Multiscale Methodology for Evaluating Distributions of Residual Stress in Processed Aerospace Alloys
(Sponsor: AFOSR)Matt Miller, Paul Dawson and Kevin McNelis, Cornell; James C. Williams, The Ohio State University
Accurate determination of residual stresses in mechanical components is a challenge that has long frustrated engineers. The conditions that cause residual stresses to exist within a component are associated with deformations that vary over the scale of the entire part, typically arising during forming when the strains and temperatures are quite inhomogeneous and becoming locked in as the part is unloaded and cools. To fully characterize the residual stress state, the part must be considered in its entirety as the stress distribution must be self-equilibrating at this scale. The stresses that persist after unloading do cause elastic strains, which are detectable by diffraction as distortions of the crystal lattice from its stress-free, natural configuration. Using high energy synchrotron X-rays these distortions can be measured within small diffraction volume throughout the part volume. Diffraction measurements provide data within crystals satisfying particular Bragg conditions, meaning that we obtain one component of strain within sets of crystals sharing a common crystallographic fiber for each data point. When combined, the data provide lattice strain pole figures and underlying distributions of lattice strain tensor distributions. The goal of this project is to develop the method to utilize the strain pole figure data pertaining to the crystal scale to determine the state of stress at the macroscopic scale, taking into account the equilibrium constraint mentioned before. At the heart of the approach is a utility for representing a distribution of the lattice strains over orientation space using a spherical harmonic expansion. Employing such a series enables us to purposefully control the degrees of freedom used to represent the distribution of lattice strains over the aggregate in a manner consistent with the available data. The figure below depicts a schematic of our formulation, which intimately couples the lattice strain pole figure measurements, the spherical harmonic expansions and the finite element discretization of the workpiece. The figure depicts the manner in which the formulation will be employed on a shrink-fit specimen - a simple example that can be used to validate the method.
Determining Stress Distributions over Deforming Polycrystals
(Sponsor: AFOSR)Tong Han, Jun-Sang Park, Hadas Ritz, Paul Dawson and Matt Miller
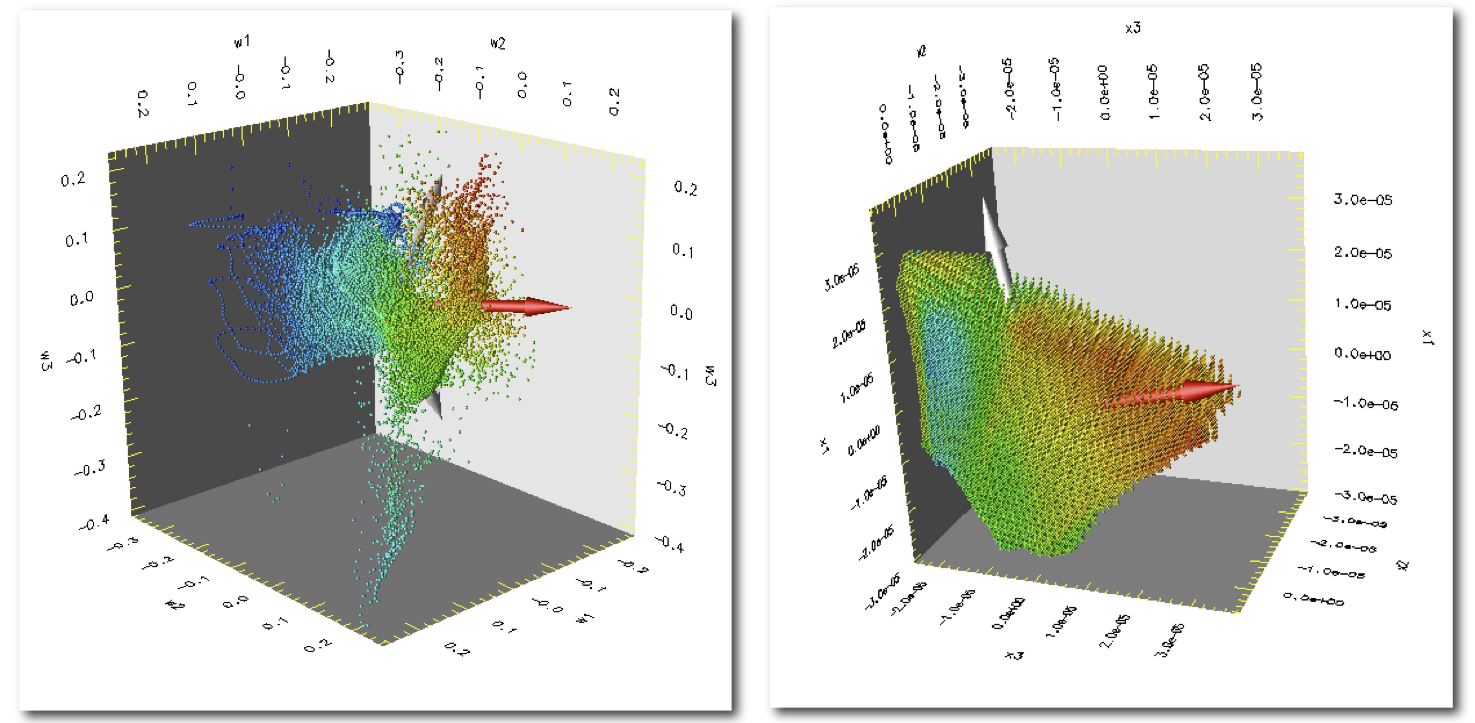
Polycrystalline materials are aggregates of single crystals whose lattice orientations vary from crystal to crystal. The mechanical properties at the crystal scale are anisotropic in both the elastic and plastic behaviors. In a typical FCC crystal, the stress required to induce plastic flow differs by more than 50% between the weakest and strongest orientations. Elastic anisotropy shows a greater range of values among common engineering alloys. Some have directional moduli that are nearly identical for all directions. In others the moduli can vary by a factor of 3 or more. Crystals are packed together to form an aggregate and collectively carry load by distributing the stress in a manner that simultaneously satisfies equilibrium and maintains compatibility. The consequence of the anisotropy in the properties is that the stress varies quite substantially over a polycrystal. This project is focused on quantifying the lattice orientation dependence of that distribution, recognizing that the distribution depends not only on the lattice orientation but also on the local surroundings of a crystal (e.g. the orientations of its neighbors). To investigate this issue, we are using combined finite element modeling and x-ray diffraction experiments with in situ loading to expose the stress distributions. Copper samples were loaded to a stress level sufficient to cause plastic flow and lattice strains were measured at several intervening load levels. The experiments were replicated using a finite element model with individually resolved grains. The first figure shows the deformed mesh with three stress components displayed. When cast over orientation space, the 'random' looking pattern from the deformed mesh exhibits an orientational dependency. This can be explained in terms of the stresses associated with vertices of the single crystal yield surface (second figure). These distribution imply the some components of the stress that are zero on-average, are non-zero and do vary systematically with orientation. The verify that the orientational dependencies computed are consistent with values associated with the measured lattice strains, we have performed an eigenfunction decomposition on each. The results shown in the third figure indicated that both experiment and simulation share the same dominant eigenmodes. This stress state develops as the plastic flow develops under monotonic straining. In the elastic regime, the stresses are not influence by the yield surface, but as the stress level increases and plasticity propagates through the polycrystal the crystal stresses rotate toward the yield surface vertices. This is quantified by the histogram shown in the final figure.
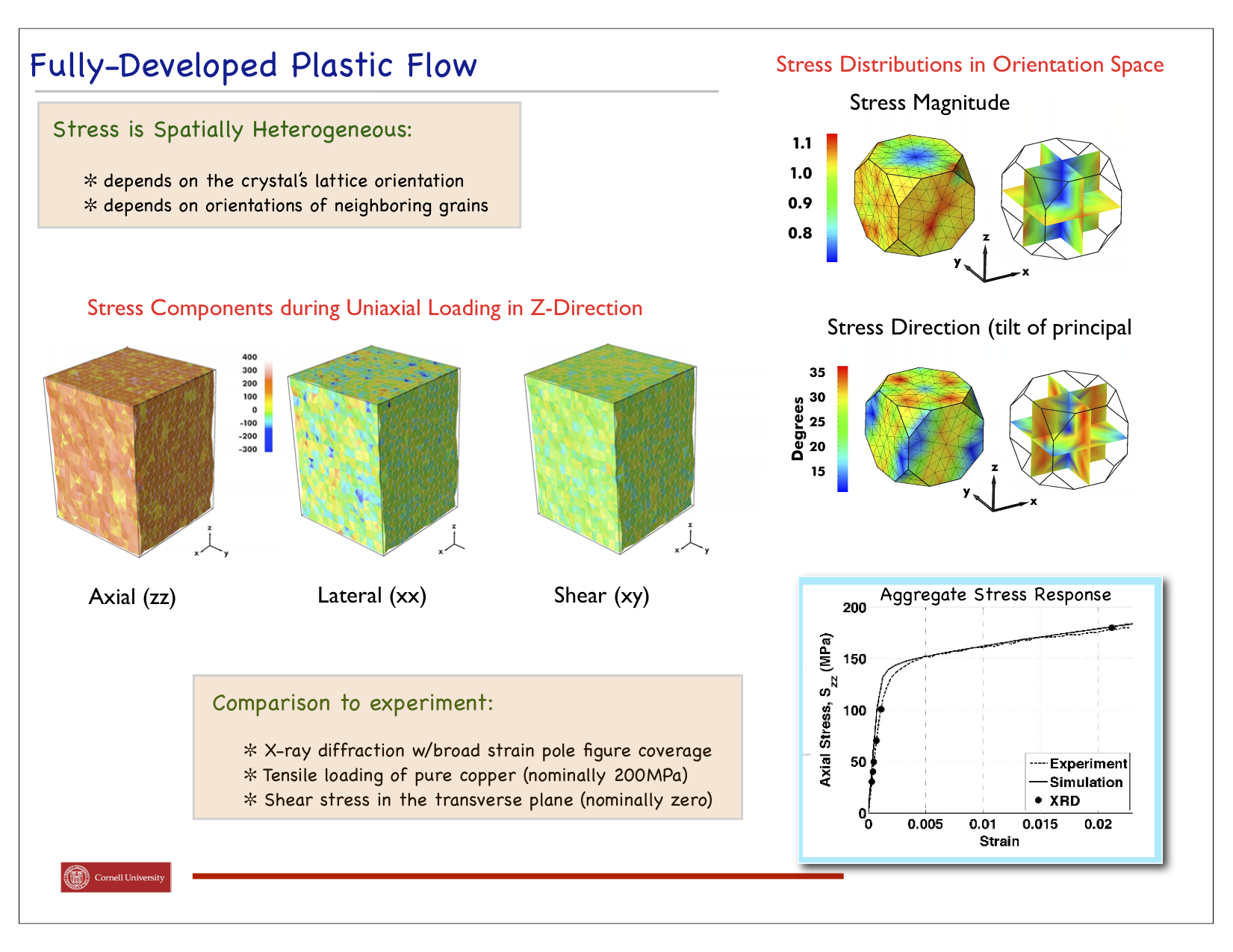
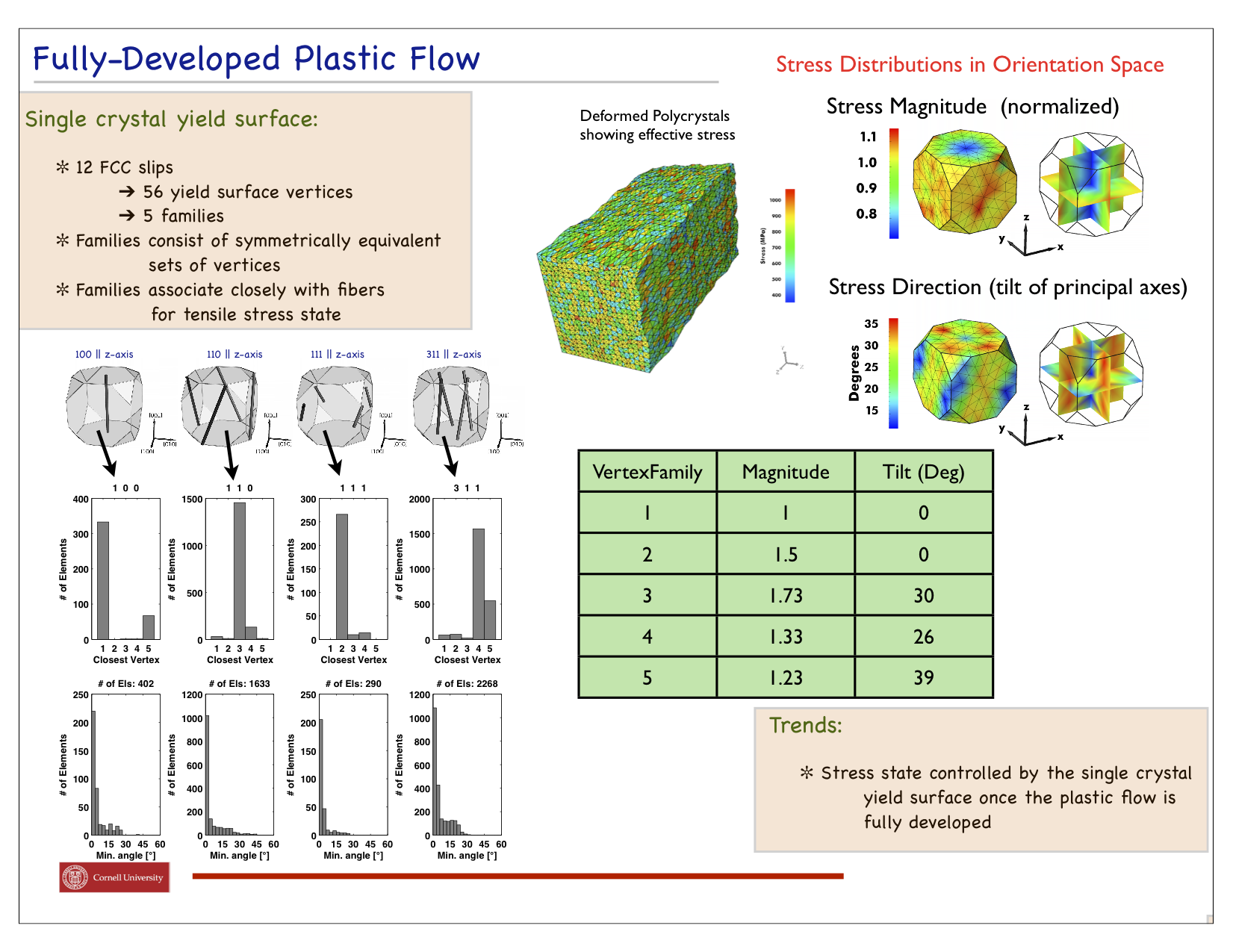

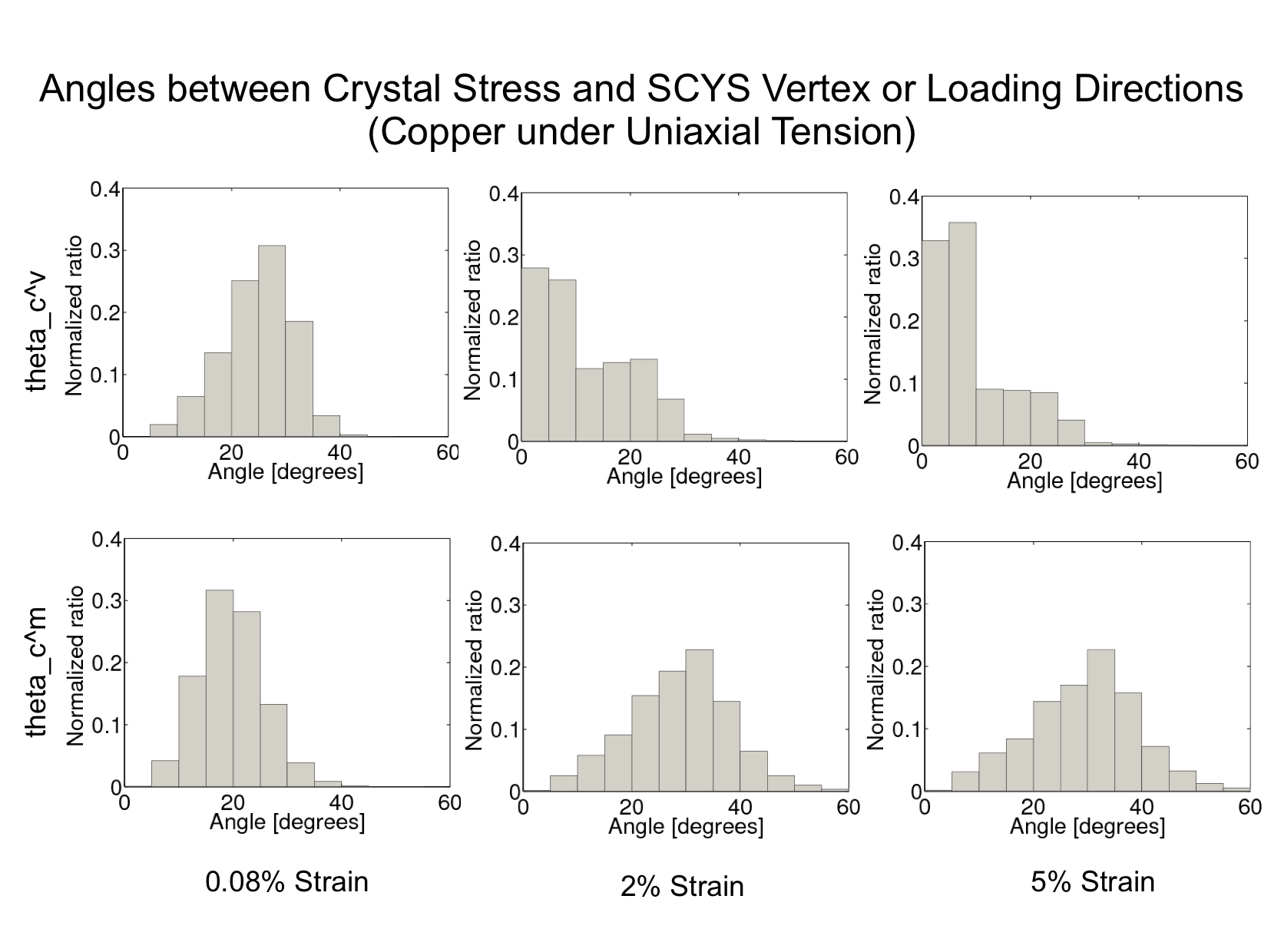
Publications related to this effort include:
- M.P. Miller, J.-S. Park, P. R. Dawson, and T.-S. Han.
Measuring and modeling distributions of stress state in deforming polycrystals.
Acta Materialia, 56:3927{3939, 2008. - H. Ritz, P. R. Dawson, and T. Marin.
Analyzing the orientation dependence of stresses in polycrystals using vertices of the single crystal yield surface.
Journal of the Mechanics and Physics of Solids, 58:54{72), 2010.